THIS PROJECT IS UNDER THE NEXT PHILOSOPHICAL PRINCIPLES
1) CONSCIOUSNESS IS INFINITE. CONVERSELY THE INFINITE IS A FUNCTION AND PROPERTY OF THE CONSCIOUSNESSES.
2) BUT THE PHYSICAL MATERIAL WORLD IS FINITE.
3) THEREFORE MATHEMATICAL MODELS IN THEIR ONTOLOGY SHOULD CONTAIN ONLY FINITE ENTITIES AND SHOULD NOT INVOLVE THE INFINITE.
THIS PROJECT THEREFORE IS CREATING AGAIN THE BASIC OF MATHEMATICS AND ITS ONTOLOGY WITH NEW AXIOMS THAT DO NOT INVOLVE THE INFINITE AT ALL.
Our perception and experience of the reality, depends on the system of beliefs that we have. In mathematics, the system of spiritual beliefs is nothing else than the axioms of the axiomatic systems that we accept. The rest is the work of reasoning and acting.
The abstraction of the infinite seems sweet at the beginning as it reduces some complexity, in the definitions, but later on it turns out to be bitter, as it traps the mathematical minds in to a vast complexity irrelevant to real life applications.
Again here is a maximum size set Ω(s). When set theory is applied to another axiomatic systems like digital real numbers or digital holographic euclidean geometry, special consideration of the relative size of Ω(s) and the resolutions of the real numbers or geometry.
A version with classes is given also. It is discussed the axiom of choice.
The Famous continuum hypothesis is discussed in the context of the digital set theory.
I do not claim here that the axioms of the digital set theory, below, are independent, in other words none of them can be proved from the others. As the elements are finite, there may be such a case. But I am strongly interested a) at first that are non-contradictory, and b) second that are adequate many, so as to describe the intended structure. later simplified and improved in elegance versions of the axioms may be given.
Here is the classical version of the Zermelo-Frankel axiomatic system of Cantors sets
We set here the presentation of the Zermelo-Frankel axiomatic system as it is in wikipedia
http://en.wikipedia.org/wiki/Zermelo%E2%80%93Fraenkel_set_theory
There are many equivalent formulations of the ZFC axioms; for a rich but somewhat dated discussion of this fact, see Fraenkel et al. (1973). The following particular axiom set is from Kunen (1980). The axioms per se are expressed in the symbolism of first order logic. The associated English prose is only intended to aid the intuition.
All formulations of ZFC imply that at least one set exists. Kunen includes an axiom that directly asserts the existence of a set, in addition to the axioms given below (although he notes that he does so only “for emphasis” (ibid., p. 10)). Its omission here can be justified in two ways. First, in the standard semantics of first-order logic in which ZFC is typically formalized, the domain of discourse must be nonempty. Hence, it is a logical theorem of first-order logic that something exists — usually expressed as the assertion that something is identical to itself, ∃x(x=x). Consequently, it is a theorem of every first-order theory that something exists. However, as noted above, because in the intended semantics of ZFC there are only sets, the interpretation of this logical theorem in the context of ZFC is that some set exists. Hence, there is no need for a separate axiom asserting that a set exists. Second, however, even if ZFC is formulated in so-called free logic, in which it is not provable from logic alone that something exists, the axiom of infinity (below) asserts that aninfinite set exists. This obviously implies that a set exists and so, once again, it is superfluous to include an axiom asserting as much.
1. Axiom of extensionality[edit]
Main article: Axiom of extensionality
Two sets are equal (are the same set) if they have the same elements.
The converse of this axiom follows from the substitution property of equality. If the background logic does not include equality "=", x=y may be defined as an abbreviation for the following formula (Hatcher 1982, p. 138, def. 1):
In this case, the axiom of extensionality can be reformulated as
which says that if x and y have the same elements, then they belong to the same sets (Fraenkel et al. 1973).
2. Axiom of regularity (also called the Axiom of foundation)[edit]
Main article: Axiom of regularity
Every non-empty set x contains a member y such that x and y are disjoint sets.
3. Axiom schema of specification (also called the axiom schema of separation or of restricted comprehension)[edit]
Main article: Axiom schema of specification
Subsets are commonly constructed using set builder notation. For example, the even integers can be constructed as the subset of the integers  satisfying the predicate
satisfying the predicate  :
:
 satisfying the predicate
satisfying the predicate  :
:
In general, the subset of a set z obeying a formula  (x) with one free variable x may be written as:
(x) with one free variable x may be written as:
 (x) with one free variable x may be written as:
(x) with one free variable x may be written as:
The axiom schema of specification states that this subset always exists (it is an axiom schema because there is one axiom for each  ). Formally, let
). Formally, let  be any formula in the language of ZFC with all free variables among
be any formula in the language of ZFC with all free variables among 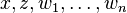 (y is not free in
(y is not free in  ). Then:
). Then:
 ). Formally, let
). Formally, let  be any formula in the language of ZFC with all free variables among
be any formula in the language of ZFC with all free variables among 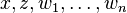 (y is not free in
(y is not free in  ). Then:
). Then:
Note that the axiom schema of specification can only construct subsets, and does not allow the construction of sets of the more general form:
This restriction is necessary to avoid Russell's paradox and its variants.
In some other axiomatizations of ZF, this axiom is redundant in that it follows from the axiom schema of replacement.
The axiom of specification can be used to prove the existence of the empty set, denoted  , once at least one set is known to exist (see above). One way to do this is to use a property
, once at least one set is known to exist (see above). One way to do this is to use a property  which no set has. For example, if w is any existing set, the empty set can be constructed as
which no set has. For example, if w is any existing set, the empty set can be constructed as
 , once at least one set is known to exist (see above). One way to do this is to use a property
, once at least one set is known to exist (see above). One way to do this is to use a property  which no set has. For example, if w is any existing set, the empty set can be constructed as
which no set has. For example, if w is any existing set, the empty set can be constructed as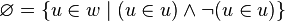 .
.
Thus the axiom of the empty set is implied by the nine axioms presented here. The axiom of extensionality implies the empty set is unique (does not depend on w). It is common to make a definitional extension that adds the symbol 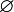 to the language of ZFC.
to the language of ZFC.
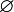 to the language of ZFC.
to the language of ZFC.4. Axiom of pairing[edit]
Main article: Axiom of pairing
If x and y are sets, then there exists a set which contains x and y as elements.
The axiom schema of specification must be used to reduce this to a set with exactly these two elements. This axiom is part of Z, but is redundant in ZF because it follows from the axiom schema of replacement, if we are given a set with at least two elements. The existence of a set with at least two elements is assured by either the axiom of infinity, or by the axiom schema of specification and the axiom of the power set applied twice to any set.
5. Axiom of union[edit]
Main article: Axiom of union
The union over the elements of a set exists. For example, the union over the elements of the set  is
is 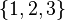 .
.
 is
is 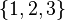 .
.
Formally, for any set  there is a set A containing every element that is a member of some member of
there is a set A containing every element that is a member of some member of  :
:
 there is a set A containing every element that is a member of some member of
there is a set A containing every element that is a member of some member of  :
:6. Axiom schema of replacement[edit]
Main article: Axiom schema of replacement
The axiom schema of replacement asserts that the image of a set under any definable function will also fall inside a set.
Formally, let  be any formula in the language of ZFC whose free variables are among
be any formula in the language of ZFC whose free variables are among 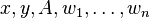 , so that in particular
, so that in particular  is not free in
is not free in  . Then:
. Then:
 be any formula in the language of ZFC whose free variables are among
be any formula in the language of ZFC whose free variables are among 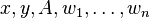 , so that in particular
, so that in particular  is not free in
is not free in  . Then:
. Then:
In other words, if the relation  represents a definable function f,
represents a definable function f,  represents its domain, and f(x) is a set for every x in that domain, then the range of f is a subset of some set
represents its domain, and f(x) is a set for every x in that domain, then the range of f is a subset of some set  . The form stated here, in which
. The form stated here, in which  may be larger than strictly necessary, is sometimes called the axiom schema of collection.
may be larger than strictly necessary, is sometimes called the axiom schema of collection.
 represents a definable function f,
represents a definable function f,  represents its domain, and f(x) is a set for every x in that domain, then the range of f is a subset of some set
represents its domain, and f(x) is a set for every x in that domain, then the range of f is a subset of some set  . The form stated here, in which
. The form stated here, in which  may be larger than strictly necessary, is sometimes called the axiom schema of collection.
may be larger than strictly necessary, is sometimes called the axiom schema of collection.7. Axiom of infinity[edit]
Main article: Axiom of infinity
Let 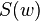 abbreviate
abbreviate  , where
, where  is some set (We can see that
is some set (We can see that  is a valid set by applying the Axiom of Pairing with
is a valid set by applying the Axiom of Pairing with  so that the set
so that the set  is
is  ). Then there exists a set X such that the empty set
). Then there exists a set X such that the empty set 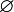 is a member of X and, whenever a set y is a member of X, then
is a member of X and, whenever a set y is a member of X, then 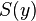 is also a member of X.
is also a member of X.
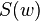 abbreviate
abbreviate  , where
, where  is some set (We can see that
is some set (We can see that  is a valid set by applying the Axiom of Pairing with
is a valid set by applying the Axiom of Pairing with  so that the set
so that the set  is
is  ). Then there exists a set X such that the empty set
). Then there exists a set X such that the empty set 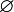 is a member of X and, whenever a set y is a member of X, then
is a member of X and, whenever a set y is a member of X, then 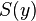 is also a member of X.
is also a member of X.
More colloquially, there exists a set X having infinitely many members. The minimal set X satisfying the axiom of infinity is the von Neumann ordinal ω, which can also be thought of as the set of natural numbers  .
.
 .
.8. Axiom of power set[edit]
Main article: Axiom of power set
By definition a set z is a subset of a set x if and only if every element of z is also an element of x:
The Axiom of Power Set states that for any set x, there is a set y that contains every subset of x:
The axiom schema of specification is then used to define the power set P(x) as the subset of such a y containing the subsets of x exactly:
Axioms 1–8 define ZF. Alternative forms of these axioms are often encountered, some of which are listed in Jech (2003). Some ZF axiomatizations include an axiom asserting that the empty set exists. The axioms of pairing, union, replacement, and power set are often stated so that the members of the set x whose existence is being asserted are just those sets which the axiom asserts x must contain.
The following axiom is added to turn ZF into ZFC:
9. Well-ordering theorem[edit]
Main article: Well-ordering theorem
For any set X, there is a binary relation R which well-orders X. This means R is a linear order on X such that every nonempty subset of X has a member which is minimal under R.
Given axioms 1–8, there are many statements provably equivalent to axiom 9, the best known of which is the axiom of choice (AC), which goes as follows. Let X be a set whose members are all non-empty. Then there exists a function f from X to the union of the members of X, called a "choice function", such that for all Y ∈ X one has f(Y) ∈ Y. Since the existence of a choice function when X is a finite set is easily proved from axioms 1–8, AC only matters for certain infinite sets. AC is characterized as nonconstructive because it asserts the existence of a choice set but says nothing about how the choice set is to be "constructed." Much research has sought to characterize the definability (or lack thereof) of certain sets whose existence AC asserts.
AN AXIOMATIC SYSTEM FOR THE DIGITAL SETS
We utilize here essentially the Zermelo-Frankel axiomatic system for set theory, but we subtract the axiom of the infinite. A second difference is that while the Zermelo-Frankel set theory is using formal logic that in its turn is using the countable infinite, we deviate from it here and we use the digital formal logic that has not any infinite in it.
(see e.g. http://en.wikipedia.org/wiki/Zermelo-Frankel_axioms )
Finally all the axioms below have the obvious exceptions when the new larger sets that their existence is claimed from previous smaller sets, exceeds the maximum acceptable (finite) cardinality Omega Ω
We have an initial relation among the sets, X belongs or is element of Y , denoted by X ε Υ
Some of these propositions are not axioms but theorems, once we have utilized as formal logic, to formulate the current set theory, with Size Ω(L) , sufficient large compared to the size of the sets of the current set theory.
0) Axiom of emty set
There exists a set with no elements
1) Axiom of extensionality
If X and Y have the same elements, then X=Y
Two sets are equal (are the same set) if they have the same elements.
The converse of this axiom follows from the substitution property of equality. If the background logic does not include equality "=", x=y may be defined as an abbreviation for the following formula (Hatcher 1982, p. 138, def. 1):
In this case, the axiom of extensionality can be reformulated as
which says that if x and y have the same elements, then they belong to the same sets (Fraenkel et al. 1973).
2) Axiom of pairing
For each two sets a, and b, there is a set {a,b} that has elements exactly the a and b.
If x and y are sets, then there exists a set which contains x and y as elements.
The axiom schema of specification must be used to reduce this to a set with exactly these two elements. This axiom is part of Z, but is redundant in ZF because it follows from the axiom schema of replacement, if we are given a set with at least two elements. The existence of a set with at least two elements is assured by either the axiom of infinity, or by the axiom schema of specification and the axiom of the power set applied twice to any set.
3) Axiom of Union
For any set X there exists a set Y=U(X), the union of all elements of X, that has as elements all elements of each element of the set X.
The union over the elements of a set exists. For example, the union over the elements of the set  is
is 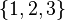 .
.
 is
is 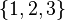 .
.
Formally, for any set  there is a set A containing every element that is a member of some member of
there is a set A containing every element that is a member of some member of  :
:
 there is a set A containing every element that is a member of some member of
there is a set A containing every element that is a member of some member of  :
:4) Axiom of Power Set
For any set X, there exists a set Y=P(X) , with elements exactly all subsets of the set X.
By definition a set z is a subset of a set x if and only if every element of z is also an element of x:
The Axiom of Power Set states that for any set x, there is a set y that contains every subset of x:
The axiom schema of specification is then used to define the power set P(x) as the subset of such a y containing the subsets of x exactly:
Axioms 1–8 define ZF. Alternative forms of these axioms are often encountered, some of which are listed in Jech (2003). Some ZF axiomatizations include an axiom asserting that the empty set exists. The axioms of pairing, union, replacement, and power set are often stated so that the members of the set x whose existence is being asserted are just those sets which the axiom asserts x must contain.
The following axiom is added to turn ZF into ZFC:
5) Axiom Schema of Replacement (or Substitution) .
If F is a logical function , then for any set Y there exists a set Z=F[Y]={F(x): x ε Y}
Theorem Schema of Separation or Comprehension (deduced from the axiom Schema of replacement)
If F is a logical property (with logical parameter p) , then for any set X and p, we can define a set Y=
{u ε X: F(u,p) is true} , that contains all those elements u of X, that have the property F.
Here is where the empty set is an existent set.
The axiom schema of replacement asserts that the image of a set under any definable function will also fall inside a set.
Formally, let  be any formula in the language of ZFC whose free variables are among
be any formula in the language of ZFC whose free variables are among 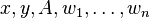 , so that in particular
, so that in particular  is not free in
is not free in  . Then:
. Then:
 be any formula in the language of ZFC whose free variables are among
be any formula in the language of ZFC whose free variables are among 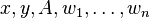 , so that in particular
, so that in particular  is not free in
is not free in  . Then:
. Then:
In other words, if the relation  represents a definable function f,
represents a definable function f,  represents its domain, and f(x) is a set for every x in that domain, then the range of f is a subset of some set
represents its domain, and f(x) is a set for every x in that domain, then the range of f is a subset of some set  . The form stated here, in which
. The form stated here, in which  may be larger than strictly necessary, is sometimes called the axiom schema of collection.
may be larger than strictly necessary, is sometimes called the axiom schema of collection.

Axiom schema of replacement: the image of the domain set A under the definable function f (i.e. the range of f) falls inside a set B. represents a definable function f,
represents a definable function f,  represents its domain, and f(x) is a set for every x in that domain, then the range of f is a subset of some set
represents its domain, and f(x) is a set for every x in that domain, then the range of f is a subset of some set  . The form stated here, in which
. The form stated here, in which  may be larger than strictly necessary, is sometimes called the axiom schema of collection.
may be larger than strictly necessary, is sometimes called the axiom schema of collection.
Every nonempty set X, has an ε-minimal element M . In other words, there is no x ε X which is element of Μ (xε Μ).
Or equivalent formulation:
Every non-empty set x contains a member y such that x and y are disjoint sets.
This implies, for example, that every set has an ordinal rank.
For any set X, there is a binary relation R which well-orders X. This means R is a linear order on X such that every nonempty subset of X has a member which is minimal under R.
Given axioms 1–8, there are many statements provably equivalent to axiom 9, the best known of which is the axiom of choice (AC), which goes as follows. Let X be a set whose members are all non-empty. Then there exists a function f from X to the union of the members of X, called a "choice function", such that for all Y ∈ X one has f(Y) ∈ Y. Since the existence of a choice function when X is a finite set is easily proved from axioms 1–8, AC only matters for certain infinite sets. AC is characterized as nonconstructive because it asserts the existence of a choice set but says nothing about how the choice set is to be "constructed." Much research has sought to characterize the definability (or lack thereof) of certain sets whose existence AC asserts.
7) Axiom of the Finite
Let 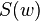 abbreviate
abbreviate  , where
, where  is some set (We can see that
is some set (We can see that  is a valid set by applying the Axiom of Pairing with
is a valid set by applying the Axiom of Pairing with  so that the set
so that the set  is
is  ).
).
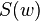 abbreviate
abbreviate  , where
, where  is some set (We can see that
is some set (We can see that  is a valid set by applying the Axiom of Pairing with
is a valid set by applying the Axiom of Pairing with  so that the set
so that the set  is
is  ).
).
Then there does not exists a set X such that whenever a set y is a member of X, then 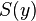 is also a member of X.
is also a member of X.
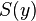 is also a member of X.
is also a member of X.
More colloquially, there does not exists a set X having infinitely many members as we have used to think.
For this concept of seemingly infinite set to work well, it is necessary to have the Good order rule of mathematical and meta-mathematical ontology , (META-MATHEMATICS MUST BE SIMPLER TO MATHEMATICS) which claims in its strongest version that a natural number of the meta-mathematical ontology, or in other words of the formal language of the axiomatic system (here of set theory) , either finite or seemingly infinite can only be finite as natural number of the objective ontology , in other words as entity of the objective ontology of the axiomatic theory (here as cardinal of a set). In its weaker version it claims simply that the largest finite and largest seemingly infinite natural number of the formal language are less correspondingly from the largest finite and largest seemingly infinite natural number of the objective ontology or in other words e.g. of cardinals of the sets. This also is the analogue in classical mathematics that we accept only at most countable infinite many symbols and well formed symbolic expressions in the formal language of the axiomatic theory.
8) Axiom of Choice
For every logical family A of nonempty sets, the domain of any choice F(A) function defines a set (A choice function has a domain the new set, that its elements are the values of the choice function F, and any argument, is a set from the family A ).
From the above we deduce that , It exists as set the Cartesian product P(S) of a set S so that every two of its elements are disjoint sets, that do not contain the empty set.
9) Axiom of the size of set theory relative to the size of the formal logic.
Τhe role of the size of the involved formal logic and the size of the set theory is similar to the role of the size of RAM memory and hard-disk memory in using a computer.
2^Ω(L)<=Ω(s).
Nevertheless in addition to the above axioms the Digital Set theory has some more axioms. But before stating the additional axioms of the digital set theory let as review the version of the Sets-classes axiomatic system initially introduced by Bernays-Goedel.
DIGITAL SET-CLASSES AXIOMATIC SYSTEM
We we have two types of entities, the sets and classes. This two kinds of objects small and big, is formulates so asto avoid the axiom schemes. We deviate from the standard axioms slightly, so as to allow only finite classes too. Again we utilize here an initial a relation of belonging ε.
FINITE LIMITATION AXIOM FOR CLASSES AND SETS. All the existential axioms below have the obvious exceptions, when the new larger classes and sets that their existence is claimed from previous smaller classes and sets, exceeds the maximum acceptable (finite) cardinality Omega Ω which is an characteristic logical and ontological property of the theory.
The value of the approach with classes it is that it avoids axiom-schemas!
A.
0) There exists the empty set
1) Any set is also a class (But a class may not be a set)
2) The Extensionality axiom holds for classes
3) If X ε Υ, then X is a set. (All elements of classes are sets)
4) The pairing axiom for sets.
B. The comprehension axiom is stated with results classes rather than sets.
For every formula F for which only set variables are quantified and for every X1, X2,...Xn sets, then it exists class Y ={x : F(x, X1,X2,...Xn)=true}.
Notice that here we deviate from the standard statement of the comprehension axiom, so as to allow only classes with finite many elements, according to the limitaion rule of maximum acceptable (finite) cardinality Omega Ω.
C. 1. Union for sets
2. Power set , for sets
3. The replacement axiom is stated here for sets producing sets in 1st order formal logic.
If F is a class and function, and X a set, then the F(x) is a set.
(Notice again here that since from the axiom of finite that we state in the next for sets, X is a finite set, so the class F(x) will be finite too)
D. Regularity axiom for sets.
Every nonempty set X, has an ε-minimal element M . In other words, there is no x ε X which is element of Μ (xε Μ).
E. Axiom of the Finite
Let 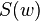 abbreviate
abbreviate  , where
, where  is some set (We can see that
is some set (We can see that  is a valid set by applying the Axiom of Pairing with
is a valid set by applying the Axiom of Pairing with  so that the set
so that the set  is
is  ).
).
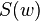 abbreviate
abbreviate  , where
, where  is some set (We can see that
is some set (We can see that  is a valid set by applying the Axiom of Pairing with
is a valid set by applying the Axiom of Pairing with  so that the set
so that the set  is
is  ).
).
Then there does not exists a set X such that whenever a set y is a member of X, then 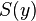 is also a member of X.
is also a member of X.
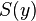 is also a member of X.
is also a member of X.
More colloquially, there does not exists a set X having infinitely many members as we have used to think.
F. Axiom of Choice.
There is a function F, such that F(Χ) εΧ for every non-empty set X.
About of the size of the class of all sets
Let us denote by Ω(s) the finite cardinal of the class of all sets and we call it the size of the set theory. Then if natural numbers are represented in the sets, and have size ω(n), and real numbers are represented in the sets and have size of high precision real numbers Ω(r), and even if the formal logic is represented in the sets, and has size Ω(L), then obviously , ω(n)<Ω(s), Ω(r)<Ω(s), Ω(L)<Ω(s).
G. Axiom of the size of set theory relative to the size of the formal logic. Spiritual and material Set Theories
The role of the size of the involved formal logic and the size of the set theory is similar to the role of the size of RAM memory and hard-disk memory in using a computer.
We diversify here to at least two types of set theories
If we claim the next axiom
2^Ω(L)<=Ω(s). The set theory is called Material Set Theory
But if we claim the next axiom
2^Ω(s)<=Ω(L). The set theory is called Spiritual Set Theory
It would very interesting of course if in the above two different versions of the axiomatic digital set theory, we would not add, in the place of the classical axiom of the infinite, the axiom of the non-existence of the infinite! Such a set theory would include the classical set theory. But for the moment we leave it as it is.
The above axiomatic set theory is categorical up to its size and size of involved (formal) logic. In other words , in the sense that any two models M1 M2 of the axiomatic digital set theory as above with equal size Ω(s), and under equal size formal logics Ω(L) are isomorphic. It is also relatively consistent to the classical Zermelo-Frankel set theory as it is easy , to construct a model of it, in the classical Zermelo-Frankel set theory.
Again in order to have a proper Digital Set-Classes axiomatic theory some more axioms are to be added.
Notice that here again both classes and sets have a finite set of elements!
So the set of all sets, it will be a class , it can be defined with a logical way, and not a set, but it will be of finite many elements! And it cannot be extended to larger class through power set or pair or union etc.
If the Digital Logic has also a maximum number of propositions and formal arguments-proofs, it is supposed that there exists a maximum number of sets to define, thus a maximum and non-changing class of all sets !!!!
It is obvious that the size Ω(L) of the involved formal Logic does affect the size of the derived set theory. if the sizes of the already existing initial (finite) sets are quite small, compared to the size of the logic that is used for the arguments on set theory, then the critical axioms like replacement , choice etc can be obtained as theorems, as the same sets can be obtained also from pair axiom or power set, union etc. But the utility of the above axioms occurs when this is not the case. In other words the sets already existing to apply the axioms of replacement choice , regularity etc are already Finite but Large compared to the size of the Logic. Also here a corresponding continuum hypothesis occurs in Digital Set Theory , if the Power set of the class of all sets, is smaller or larger that the size Ω(L) of the logic, and similar comparisons with the size of the axiomatic system of natural numbers that is standardized within the digital set theory, and the density or resolution of the digital real Numbers that is standardized within digital set theory.
It is discussed the well known fact, that there are two natural orders in the sets, the inclusion (subset) and the e-(belonging) order. For the finite sets, of natural mathematics (axiomatic digital mathematics), these two orders give a revealing explanation, of why sets, are so much used in mathematics.
It is interesting to remark, that a relaxation of the axioms of Digital set theory, which is the Classical ZFC-set theory, with the axiom of infinite replaced with its negation , the axiom of the finite, , thus accepting unbounded finite sets only, is equiconsistent with the classical Peano axiomatic system of the classical natural numbers (not the digital natural numbers) . (see e.g. http://en.wikipedia.org/wiki/Peano_axioms ).
How von Neumann created all the natural numbers, from sets and the nothingness (empty set)
| First few von Neumann ordinals | ||
|---|---|---|
| 0 | = Ø | |
| 1 | = { 0 } | = {Ø} |
| 2 | = { 0, 1 } | = { Ø, {Ø} } |
| 3 | = { 0, 1, 2 } | = { Ø, {Ø} , {Ø, {Ø}} } |
| 4 | = { 0, 1, 2, 3 } | = { Ø, {Ø}, {Ø, {Ø}}, {Ø, {Ø}, {Ø, {Ø}}} } |
References
1) T. Jech Set theory Academic Press 1978
2) A.A. Fraenkel’s Abstract Set theory (Series Studies in Logic) )North Holland 1953
We will prove in this chapter that somehow the digital Set theory is a part of the digital Logic, as the sets correspond essentially to logical formulas. Thus a triumph here of the Logic-ism approach of Frege.
It is also discussed the timelines of the set theory (Set might but classically do not have birthdays....) Sets correspond to what can be created from a finite population civilization in finite time, that may be thousands and millions of years.
At the end of this chapter, there is
a) Advantages-disadvantages of these new digital mathematics compared to the classical analogue, infinitary mathematics.
b) A fictional discussion in dialogue form of celebrated historic creators of the old mathematics praising or questioning the new mathematics compared to the old.
Speakers
Pythagoras, Euclid, Newton, Weierstrass, Cantor, Frege etc
Pythagoras is much asking Cantor, why he thinks that numbers are not adequate to be the elementary creating entities for all othe entities in mathematics (arithmo-genic (=number-generated) mathematics. Cantor insists that the partial order, is the appropriate elementary structure and not the linear well order of the natural numbers.
![\forall x \forall y [ \forall z (z \in x \Leftrightarrow z \in y) \Rightarrow x = y].](https://upload.wikimedia.org/math/0/a/8/0a8b32e152b4767f261873ebb1979987.png)
![\forall z [ z \in x \Leftrightarrow z \in y] \land \forall w [x \in w \Leftrightarrow y \in w].](https://upload.wikimedia.org/math/f/3/5/f3571ea45b17e52b1017731edf437f42.png)
![\forall x \forall y [ \forall z (z \in x \Leftrightarrow z \in y) \Rightarrow \forall w (x \in w \Leftrightarrow y \in w) ],](https://upload.wikimedia.org/math/2/c/4/2c4ed9ce024367e279071dfc5a023ae0.png)
![\forall x [ \exists a ( a \in x) \Rightarrow \exists y ( y \in x \land \lnot \exists z (z \in y \land z \in x))].](https://upload.wikimedia.org/math/f/a/5/fa52464be831688b2e2043734c3bda0e.png)


![\forall z \forall w_1 \forall w_2\ldots \forall w_n \exists y \forall x [x \in y \Leftrightarrow ( x \in z \land \phi )].](https://upload.wikimedia.org/math/7/0/1/701dced28f1c4af36e8426588768b32f.png)


![\forall \mathcal{F} \,\exists A \, \forall Y\, \forall x [(x \in Y \land Y \in \mathcal{F}) \Rightarrow x \in A].](https://upload.wikimedia.org/math/9/5/0/950d9c9aed253bc82c5df4330ca87125.png)
![\forall A\forall w_1 \forall w_2\ldots \forall w_n \bigl[ \forall x ( x\in A \Rightarrow \exists! y\,\phi ) \Rightarrow \exists B \ \forall x \bigl(x\in A \Rightarrow \exists y (y\in B \land \phi)\bigr)\bigr].](https://upload.wikimedia.org/math/4/f/d/4fd3e8bc034d26381b5b6d3f7be6d067.png)
![\exist X \left [\varnothing \in X \and \forall y (y \in X \Rightarrow S(y) \in X)\right ].](https://upload.wikimedia.org/math/0/4/a/04a649153aa8f4e3aa90ea6ac91d13ff.png)
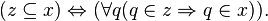
![\forall x \exists y \forall z [z \subseteq x \Rightarrow z \in y].](https://upload.wikimedia.org/math/7/4/4/7449b12272341501f69cc30e878c294b.png)

